Continue Iterating Until pn pn 1 10 5
One of the many real-world uses for Newton's Method is calculating if an asteroid will encounter the Earth during its orbit around the Sun.
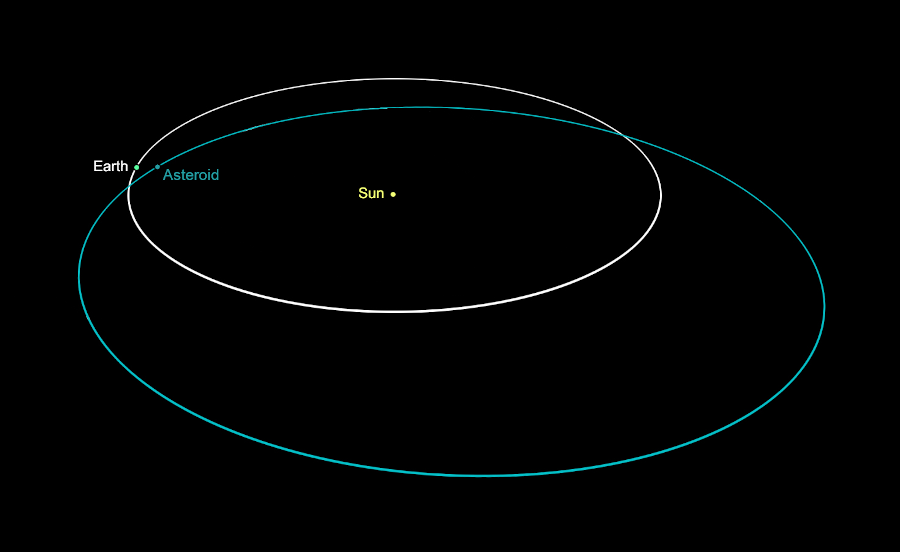
The Earth's elliptical orbit (white) and an asteroid's elliptical orbit (blue) around the Sun
All objects in orbit around the Sun have an elliptical orbit, where the size and shape of the ellipse are unique to each respective astronomical object. The standard equation form for an ellipse is given as:
$$ \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 $$
Since an ellipse is represented by this nonlinear equation form and the path of the Earth and asteroid are each represented by their own unique ellipse equation, the two objects' paths around the Sun are in fact a system of nonlinear equations which can be solved to find intersection points.
Typically, we learn Newton's Method in the context of finding the roots/zeroes of an equation. However, Newton's Method is so powerful that it can also be used to solve a system of equations, linear and nonlinear.
Once we are comfortable using Newton's Method for a single equation, we can set up a modified version of the method to solve our Earth/asteroid system of nonlinear ellipse equations. If any intersection points are found, we can use other orbital mechanics equations to determine when each object will reach those intersection points.
If there are no intersection points, the asteroid will not encounter the Earth. If there are intersection points but the asteroid and Earth reach them at different times, the asteroid will not encounter the Earth. If there are intersection points and the asteroid and Earth do reach them at the same time, the asteroid could encounter the Earth.
The general equation for Newton's Method is given as:
$$x_{i + 1} = x_{i} \; – \; \frac{f(x_{i})}{f'(x_{i})}; \; i=0, 1, 2…$$
Where xi + 1 is the x value being calculated for the new iteration, xi is the x value of the previous iteration, f(xi) is the function's value at xi , and f '(xi) is the value of the function's derivative at xi .
For the first iterationi = 0 we will plug0 in for iin the general equation. This results in:
$$x_{(0) + 1} = x_{(0)} \; – \; \frac{f(x_{(0)})}{f'(x_{(0)})} \; \Rightarrow \; x_{1} = x_{0} \; – \; \frac{f(x_{0})}{f'(x_{0})}$$
To begin the calculation process, we must decide on an initial guess of the root which we will call x0 . The initial guess can be any real number but keep in mind that the closer our initial guess is to the actual root of the function, the more likely we are to find a solution quickly.
Then, evaluate the function and its derivative atx = x0. Plug x0 , f(x0), and f '(x0) into the equation to find x1 . We have now completed the first iteration and must determine if more iterations are necessary.
To determine if more iterations are necessary, we use the following convergence criteria formulas:
$$\lvert x_{i + 1} \; – \; x_{i} \rvert \leq \varepsilon \; \text{ and } \; \lvert f(x_{i + 1}) \rvert \leq \delta $$
Where xi + 1 is the x value being calculated for the new iteration, xi is the x value of the previous iteration, ε is the desired precision (closeness of successive x values), f(xi+1) is the function's value at xi+1 , and δ is the desired accuracy (closeness of approximated root to the true root).
We must decide on the value of ε and δ and leave them constant during the entire run of iterations. The smaller these values are, the more precise and accurate our solution will be. However, if we set the values too small, it could take an excessive amount of iterations to satisfy the convergence criteria.
Now, we check if the convergence criteria have been satisfied by plugging the values of the respective variables into each of the two convergence criteria formulas. For the first iterationi = 0, this will look like:
$$ \begin{align} & \lvert x_{(0)+1} \; – \; x_{(0)} \rvert \leq \varepsilon \; \Rightarrow \; \lvert x_{1} \; – \; x_{0}\rvert \leq \varepsilon \\ \\ & \lvert f(x_{(0) \; + \; 1}) \rvert \leq \delta \; \Rightarrow \; \lvert f(x_{1}) \rvert \leq \delta \end{align}$$
For the convergence criteria to be satisfied, the inequalities in each of the formulas must be true. If one of the inequalities is true but the other is not, convergence has not been met and iteration must continue until the convergence criteria have been satisfied.
If the convergence criteria have been satisfied on a given iteration, calculations are stopped and the x value for that iteration is taken as the solution.
Sometimes Newton's Method will diverge away from a solution and the convergence criteria will never be satisfied. This may happen in any number of iterations. If using a computer to solve with Newton's Method, it is important to set a maximum number of iterations such that calculations will be stopped before a potentially infinite number of iterations occur.
Source: https://www.voovers.com/calculus/newtons-method-calculator/
0 Response to "Continue Iterating Until pn pn 1 10 5"
Post a Comment